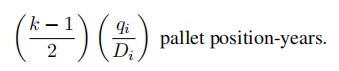Aisles provide accessibility, not storage, and so this space for aisles is not directly revenue-generating. Consequently we prefer to reduce aisle space to the minimum necessary to provide adequate accessibility. For this the aisles must be at least wide enough for a forklift to insert or extract a pallet.
By storing product in lanes, additional pallet positions can share the same aisle space and so amortize that cost. Should lanes be four pallets deep? Six? Ten? There are many issues to consider, but the most important one is effective utilization of space. For example, double-deep layout (lanes that are two pallet-positions deep) fifits about 41% more pallet positions in the same flfloor area than does single-deep layout in the example of Figure 6.3; but is it a better layout? Are enough of the additional pallet positions usefully engaged? There is a trade-off: The single-deep layout has eight aisles and provides 196 pallet storage locations, all of which are directly accessible, which means that they are available for reassignment as soon as the current pallet is shipped out.
Figure 6.3: 1-deep versus 2-deep storage
In contrast, the double-deep layout has only six aisles and provides 280 pallet storage locations—but only 140 of them are directly accessible. Moreover, the 140 that are directly accessible are not available for reuse until the interior pallet location in the same lane becomes available. S Deeper lanes produce more pallet storage locations but they are of diminishing value.
By pallet position we mean the flfloor space required to hold a pallet. This includes not only the footprint of the pallet but also any required gap between one pallet and an adjacent one (Figure 6.4). Let the lanes be k pallet positions deep. Each lane requires aisle space at its head so that pallets can be inserted and removed. Let the aisle space in front of the pallet be of area a, measured in pallet positions. Then the total area charged to one lane is k + a/2 pallet positions. This area is the sum of space devoted to storage (k) and space that provides accessibility (a/2).
Figure 6.4: The flfloor space charged to a lane includes storage space, any gap between lanes, and one-half the aisle width in front of the lane.
In most warehouses a lane is dedicated entirely to a single SKU to avoid double-handling pallets. This saves time but incurs a cost in space: When the fifirst pallet is retrieved from a lane, that position is unoccupied but unavailable to other SKUs. The deeper the lane, the greater this cost. The fifirst pallet position in a k-deep lane that holds uniformly moving product will be occupied only 1/k of the time, the second 2/k of the time, and so on (Figure 6.4). This waste is called honeycombing. Deeper lanes are more susceptible to honeycombing; but shallow lanes use more space for accessibility.
Table 6.1: Four pallet positions of a SKU with constant demand are arranged in various lane depths. The area that is unoccupied but unusable by other SKUs is waste. Area is measured in pallet positions; and a is the width of the aisle, measured as a fraction of the depth of a pallet position.
Table 6.1 displays daily snapshots of a SKU with an order size that occupies four pallet positions and which is extracted at a rate of one pallet-position per day. In single-deep rack, all the unused space is the aisle space required for accessibility. Deeper aisles require less aisle space per pallet position — but the additional pallet positions are less fully occupied.
To maximize space effificiency SKU i should be stored in a lane of depth that mini-mizes floor space-time that is unoccupied but unavailable to other SKUs. The optimum lane depth can be determined by simply evaluating all possibilities, as has been done in Table 6.1. In Figure 6.5 waste has been plotted for each lane depth, and it can be seen that 2-deep lanes are most space effificient when the aisle is less than 4 pallet positions wide; otherwise 4-deep is best.
Figure 6.5: Waste, measured as pallet position-days that are unoccupied but unavailable, depends on both the lane depth and the aisle width. The four pallets of this SKU should be stored either 2-deep or else 4-deep, depending on the width of the aisle.
If an approximate answer is acceptable then there is an easier way to compute a lane depth that is space effificient. Suppose that SKU i experiences constant demand of Di pallets annually and that the order quantity is qi pallets, so that a pallet departs every 1/Di years and the order cycle is of duration qi/Di years.
Assume the pallets of SKU i are stackable in columns zi high so that a full allotment of SKU i will require dqi/zie floor positions. Another column of pallets will be gone and a floor position will become unoccupied after every zi/Di
time periods.
If lanes are k positions deep then SKU i will require dqi/ (zik)e lanes. Each lane will have an additional pallet position on the floor that is unoccupied but unavailable after time intervals of 1zi/Di, 2zi/Di, 3zi/Di
, . . . , (k k 1) zi/Di
, for a waste of zik (k k 1) / (2Di) pallet position-years per lane. If we approximate the number of lanes by qi/ (zik) and multiply this times the waste per lane, we get an approximation of the total waste due to (horizontal) honeycombing during one inventory cycle:
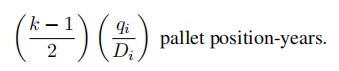
The other type of unoccupied space is that devoted to accessibility and we may charge each lane a/2 pallet positions per time period for this. The fifirst lane will be depleted and available for reassignment after kzi
time periods, the second after 2kzi time periods, and so on. If there are a total of qi/ (zik) lanes, then there are
lane-years, each to be charged a/2 pallet positions per lane, for a total accessibility cost per cycle of
The total space lost from storage during this inventory cycle is the sum of the honey-combing and accessibility costs; and the average cost per unit time is the total cost per cycle divided by the duration of an inventory cycle, which is qi/Di:
Theorem 6.1 (Optimal Lane-Depth). The most space-effificient lane depth for SKU i with qi pallets stackable zi high is
Proof. Differentiating the total cost (Expression 6.1) with respect to k, setting equal to zero, and solving for k gives the result.
This theorem gives an ideal lane depth for SKU i. It is an ideal because it ignores the space constraints imposed by the physical layout of the warehouse, so it should be taken as advisory. Also, this is an approximate answer because we avoided combinatorial complications by treating the number of lanes as qi/ (zik), which is possibly fractional.
It would be impractical to allow each SKU in a warehouse to choose its own lane depth, because the resulting assortment of lanes might not fit well together within the warehouse. Instead, one typically forces a community of SKUs to choose jointly a single lane depth that all will share. Let there be n SKUs; then:
Theorem 6.2 (Floor storage). To minimize the average flfloor space consumed per pallet, floor storage should be confifigured with lane depth of approximately
In other words, the most space effificient lane depth is of the form:
Proof. If all SKUs adopt the same lane depth k, the total average cost per unit time, from summing Expressions 6.1, is
Taking the derivative with respect to k, setting it to zero, and solving for k yields the result.
Example 6.1. Consider the following population of SKUs:
What is the optimal lane depth in flfloor storage if aisles are 15 feet across (about 4.6 meters) and the pallets are 48 inches deep and 42 inches wide (1.22 meters by 1.07 meters)?
First, convert the unit of measure for aisle width to “pallet depths”: 15 feet represents 15/ (48/12) = 3.75 pallet positions. Substituting into Expression 6.3 gives
so lanes should be about fifive pallet positions deep.
Let us pause to assess the model. First note that it is based on the assumption that each SKU moves at a relatively constant rate. If this does not hold, such as for highly seasonal SKUs, then we must estimate, based on forecast movement velocities, a weighted average of the wasted space within a lane.
Another important observation is that this model applies however the pallets leave, whether intact or picked carton-by-carton.
It should also be noted that the approximation that enables the simple, continuous solution of Theorem 6.2 will be most accurate when there are relatively large numbers of pallets of each SKU. On the other hand, when there are few pallets of each SKU then lane depth is not an issue.
It is also worth remarking that this model is designed to reduce space that is unoccupied but unavailable for storage. It is a slightly different problem to determine how many pallet positions the warehouse should have. To answer this requires more detailed information, such as time series of expected quantities of each SKU. The answer depends heavily on correlations amongst the inventory levels and the aversion to risk of under- or over-fifilling the warehouse.
Finally, this analysis says nothing about how the aisles should be arranged within the warehouse. In effect it assumes that the warehouse is large so that edge effects are negligible.
We can perform similar analysis for rack storage. Consider, for example, pallet flow rack confifigured to a common height of z pallet openings. If each opening holds at most one pallet of any SKU, then we fifind that again the optimum lane depth follows the form of Expression 6.4:
Theorem 6.3 (Pallet flflow rack). To minimize the average flfloor space consumed per pallet, pallet flflow rack should be confifigured with lane depth of approximately
Proof. Left as an exercise: See Question 6.14
.